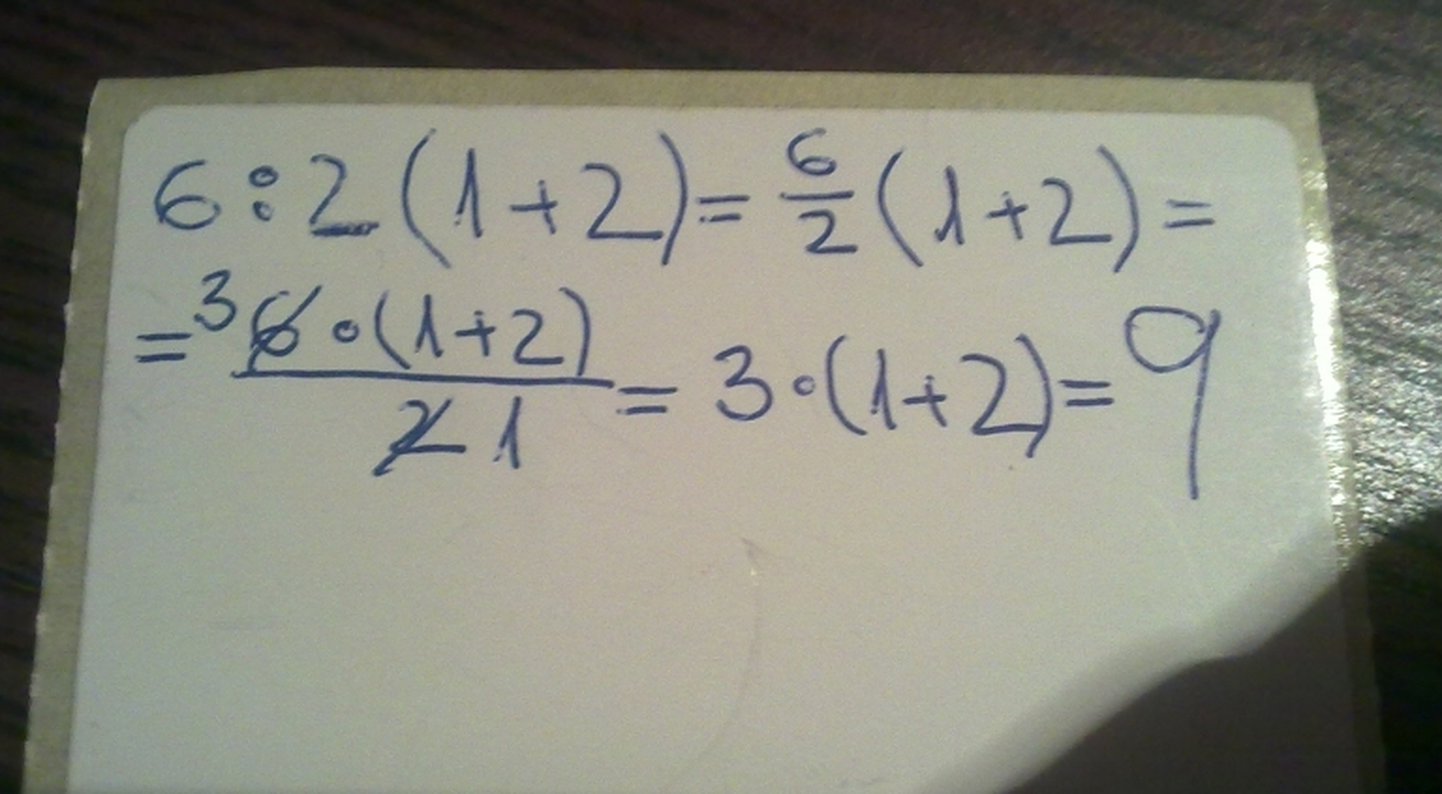
Juba pikemat aega käib erinevates foorumites äge vaidlus, et mis on 6÷2(1+2) vastuseks. Raskusi on inimestele valmistanud tehete järjekord. Tartu Miina Härma gümnaasiumi matemaatikaõpetaja Tiiu Sasi selgitab, kuidas ülesannet tuleb lahendada.
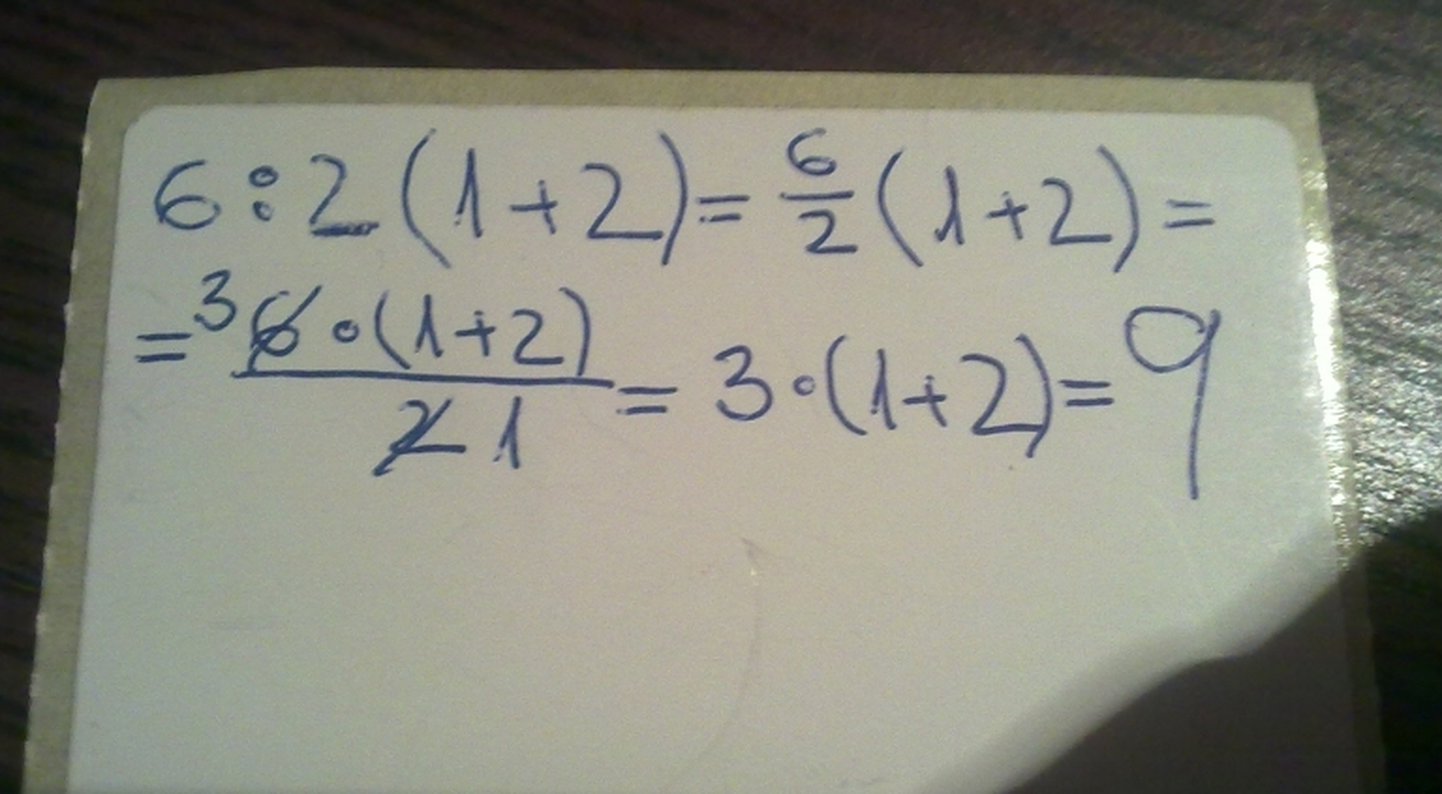
Juba pikemat aega käib erinevates foorumites äge vaidlus, et mis on 6÷2(1+2) vastuseks. Raskusi on inimestele valmistanud tehete järjekord. Tartu Miina Härma gümnaasiumi matemaatikaõpetaja Tiiu Sasi selgitab, kuidas ülesannet tuleb lahendada.
Tartu Miina Härma gümnaasiumi matemaatikaõpetaja Tiiu Sasi selgitus:
Matemaatikas on tehete järjekorra reegel, et enne korrutame ja jagame, siis liidame ja lahutame. Ja võrdväärsed tehted teeme vasakult-paremale.
Järelikult:
6:2+3= 3+3=6
12 : 2 *3=6*3=18
2+6:3= 2+2=4
6:2 + 9:3=3+3=6
Kui tahame tehete järjekorda muuta, siis lisame sulgusid. Sulgudes tuleb tehted esimesena teha.
6:(2+3)=6:5=1,2
12:(2*3)=12:6=2
Antud ülesande puhul oleks ülesanne ilma sulgude lisamiseta 6:2*1+2= 3*1+2=3+2=5
Kui on lisatud sulud, siis saame tehete järjekorda muuta 6:2*(1+2)=6:2*3=3*3=9
Kui soovime, et jagamistehe oleks viimane, peaksime lisama juba kahed sulud 6:[2*(2+1)]=6:[2*3]=6:6=1
Korrutusmärk on märk, mis jäetakse matemaatikas tihti kirjutamata(kokkuleppeliselt), kuid tema kirjutamine või mitte kirjutamine ei muuda kindlasti tehete järjekorda.
Ka kaldkriips jagamismärgina ei ole nii võimas, et tähendaks, et kõigega, mis talle järgneb tuleb jagada. Jagada tuleb vaid selle arvu või tähega, mis talle vahetult järgneb.
2/3a= 2:3*a= VAATA PILTI 2
Kui soovime, et jagataks 3a-ga, siis kirjutame 2/(3a)= VAATA PILTI 2
Tehete järjekord on tähtis selleks, et me saaksime üksteisest täpselt aru. Ka arvutitega, pangaautomaatidega suheldes on tähtis, et me annaksime arvutile üheselt mõistetava käsu.
Mingit sõna edastades, tuleb selles tähtede järjekord õigesti kirjutada : näiteks salasõna kirjutades, ei tohi ühegi tähega eksida. Kui eksime, võime saada hoopis midagi muud: midagi sellist, mida sugugi ei soovinud. Ja süüdistada võime vaid ennast.
Matemaatika ongi selline teadus, mis võimaldab meid ennast täpselt(üheselt) väljendada.
Täpne eneseväljenduse oskus on tulevikuinimesele aga tähtis- kuna me tihti ei saa suhelda teise inimesega silmast-silma, kasutada kehakeelt ja erinevaid kõnetoone, vaid peame edastama oma sõnumi kirjalikult, arvuti abil.
Täpsusest muidugi üksi ei piisa- on vaja ka mõistetavust. Me võime olla väga täpsed, kuid teised inimesed ei mõista meid.
Seetõttu on kokkulepitud ühtsed reeglid, näiteks et « +» märk tähendab liitmist, et tehteid teeme kõik sellises järjekorras ja paneme kirja sellisel viisil.
Muidugi on erinevates riikides kasutusel veidi erinev sümboolika, kuid seda tuleb teada ja arvestada niikaua kui ühtselt pole kokku lepitud. Sama on ka erinevate keelte ja ka näiteks rahaga. Matemaatikas on ühtseid kokkuleppeid sümboolikas palju, kuna seda sümboolikat on vaja mõista paljude teiste teaduste inimestel peale matemaatikute.